Geometric utilities

Main author: Simon Rohou

Alignment and orientation

The following functions provide reliable outputs for alignement evaluations.

BoolInterval codac2::aligned(const IntervalVector &p1, const IntervalVector &p2, const IntervalVector &p3)

Checks whether three 2D points are aligned (colinear).

Determines if the points lie on the same straight line using an orientation test (cross product). Depending on floating point uncertainties, the test may not be able to conclude (a UNKNOWN value would then be returned).

Parameters:

p1 – First point (2d IntervalVector) of the triplet.
p2 – Second point (2d IntervalVector) of the triplet.
p3 – Third point (2d IntervalVector) of the triplet.

Returns:

A BooleanInterval

a = aligned([0,0],[1,1],[10,10])
# a == BoolInterval.TRUE
b = aligned([0,0],[1.1,1.1],[10,10])
# b == BoolInterval.UNKNOWN (due to floating point uncertainty)

p1, p2, p3 = IntervalVector([0,0]), IntervalVector([0,1]), IntervalVector([10,10])
c = aligned(p1,p2,p3)
# c == BoolInterval.FALSE

BoolInterval a = aligned({0,0},{1,1},{10,10});
// a == BoolInterval::TRUE
BoolInterval b = aligned({0,0},{1.1,1.1},{10,10});
// b == BoolInterval::UNKNOWN (due to floating point uncertainty)

IntervalVector p1({0,0}), p2({0,1}), p3({1,10});
BoolInterval c = aligned(p1,p2,p3);
// c == BoolInterval::FALSE

OrientationInterval codac2::orientation(const IntervalVector &p1, const IntervalVector &p2, const IntervalVector &p3)

Computes the orientation of an ordered triplet of 2D points.

Determines whether the oriented angle \(\widehat{p_1 p_2 p_3}\) is positive (counterclockwise), negative (clockwise), or if the points are colinear (flat or 0 angle). Depending on floating point uncertainties, the test may not be able to conclude (a UNKNOWN value would then be returned).

Parameters:

p1 – First point (2d IntervalVector) of the triplet.
p2 – Second point (2d IntervalVector) of the triplet (vertex of the angle).
p3 – Third point (2d IntervalVector) of the triplet.

Returns:

An orientation of type OrientationInterval

a = orientation([0,0],[1,1],[10,10])
# a == OrientationInterval.COLINEAR
b = orientation([0,0],[1.1,1.1],[10,10])
# b == OrientationInterval.UNKNOWN (due to floating point uncertainty)

p1, p2, p3 = IntervalVector([0,0]), IntervalVector([1,1]), IntervalVector([-1,2])
c = orientation(p1,p2,p3)
# c == OrientationInterval.CLOCKWISE
d = orientation(p3,p2,p1)
# d == OrientationInterval.COUNTERCLOCKWISE

OrientationInterval a = orientation({0,0},{1,1},{10,10});
// a == OrientationInterval::COLINEAR
OrientationInterval b = orientation({0,0},{1.1,1.1},{10,10});
// b == OrientationInterval::UNKNOWN (due to floating point uncertainty)

IntervalVector p1({0,0}), p2({1,1}), p3({-1,2});
OrientationInterval c = orientation(p1,p2,p3);
// c == OrientationInterval::CLOCKWISE
OrientationInterval d = orientation(p3,p2,p1);
// d == OrientationInterval::COUNTERCLOCKWISE

Convex hull

std::vector<IntervalVector> codac2::convex_hull(std::vector<IntervalVector> pts)

Computes the convex hull of a set of 2d points.

Given a set of 2d points enclosed in tiny boxes, the function computes their convex hull. The method is based on a Graham scan algorithm. The output list of the algorithm is a subset of the input list, with same uncertainties and a possible different order.

Parameters:: pts – 2d points in any order
Returns:: Points on the convex hull in counterclockwise order.

v = [
  [0,3],[1,1],[2,2],[3.5,3.5],
  [0.5,1.2],[1,2],[3,1],[3,3],
  [1,3.5],[2.5,4],[0.1,2.7],[3.2,3.6]
]

hull = convex_hull(v);
# hull == [ [1,1], [3,1], [3.5,3.5], [2.5,4], [1,3.5], [0,3], [0.5,1.2] ]

vector<IntervalVector> v {
  {0,3},{1,1},{2,2},{3.5,3.5},
  {0.5,1.2},{1,2},{3,1},{3,3},
  {1,3.5},{2.5,4},{0.1,2.7},{3.2,3.6}
};

vector<IntervalVector> hull = convex_hull(v);
// hull == { {1,1}, {3,1}, {3.5,3.5}, {2.5,4}, {1,3.5}, {0,3}, {0.5,1.2} }

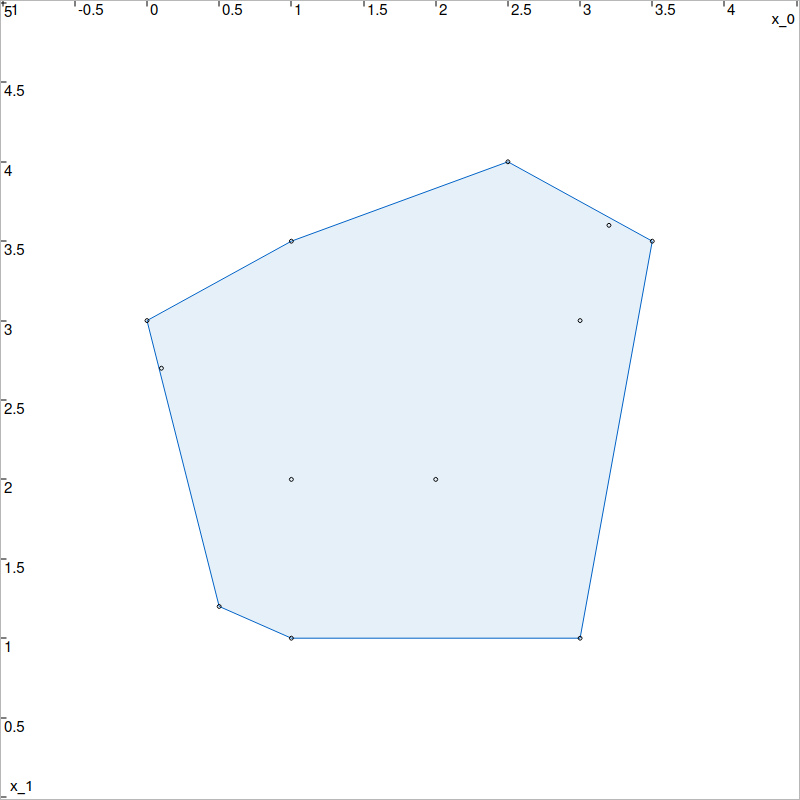
../../_images/convex_hull_example.png — Convex hull of a set of points.

Geometric operations on objects

template<typename T> inline T codac2::rotate(const T &x, const Interval &a, const IntervalVector &c = Vector::zero(2))

Rotates a 2D object (Segment, Polygon, etc) around a point by a given angle.

This function performs a 2D rotation of the input object x by an interval angle a, optionally around a center of rotation c (default is the origin). This operation propagates uncertainties through interval arithmetic.

Parameters:

x – The input 2D object to be rotated.
a – The rotation angle as an interval (in radians).
c – The center of rotation as an interval vector (default is the origin (0,0)).

Returns:

The rotated object.

void codac2::merge_adjacent_points(std::list<IntervalVector> &l)

Merges overlapping or adjacent IntervalVector points within a list.

This function iteratively scans a list of IntervalVector objects and merges any pairs that intersect. The process repeats until no further merges are possible.

This operation is useful for simplifying collections of intervals or bounding boxes that may overlap due to uncertainty propagation or geometric tolerance.

Parameters:: l – list of IntervalVector objects to be merged. The list is modified in-place.