The CtcPolar contractor
Main authors: Benoît Desrochers, Simon Rohou
-
class CtcPolar : public codac2::Ctc<CtcPolar, IntervalVector>
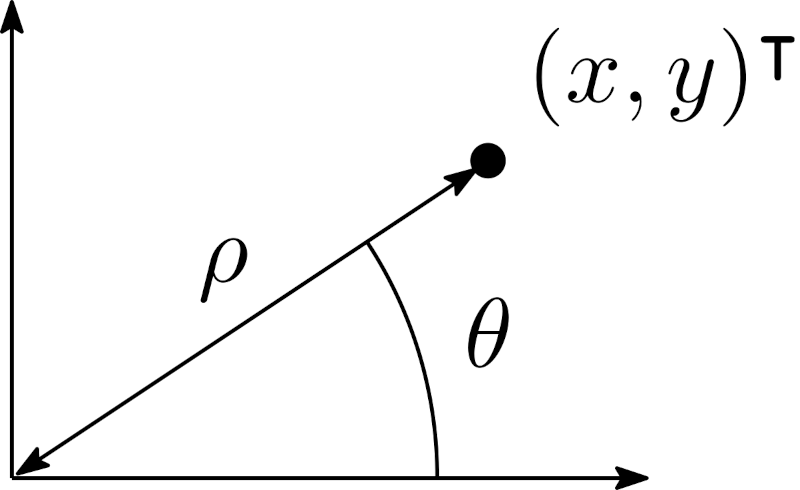
Implements the polar constraint on \(x\in\mathbb{R}\), \(y\in\mathbb{R}\), \(\rho\in\mathbb{R}^+\) and \(\theta\in\mathbb{R}\) such that:
\[\begin{split}\left\{~\begin{array}{lll}x&=&\rho\cos\theta\\y&=&\rho\sin\theta\end{array}\right. \end{split}\]The contractor can be applied either on a 4d box or on a set of four intervals.
This contractor is minimal.
In robotics, it can be used to express a range-and-bearing constraint. It can be seen as an extension of \(\mathcal{C}_{\textrm{dist}}\) enriched with the bearing information.
Methods
-
void codac2::CtcPolar::contract(IntervalVector &x) const
Applies \(\mathcal{C}_{\textrm{polar}}\big([\mathbf{x}]\big)\).
- Parameters:
x –
IntervalVectorfor \((x,y,\rho,\theta)^\intercal\)
x = IntervalVector([[5,6.5],[6.5,8],[10,11],[0.8,1]])
c = CtcPolar()
x = c.contract(x)
# x = [ [6, 6.5] ; [7.59934, 8] ; [10, 10.3078] ; [0.863211, 0.927296] ]
IntervalVector x({{5,6.5},{6.5,8},{10,11},{0.8,1}});
CtcPolar c;
c.contract(x);
// x = [ [6, 6.5] ; [7.59934, 8] ; [10, 10.3078] ; [0.863211, 0.927296] ]
-
void codac2::CtcPolar::contract(Interval &x, Interval &y, Interval &rho, Interval &theta) const
Applies \(\mathcal{C}_{\textrm{polar}}\big([x],[y],[\rho],[\theta]\big)\).
- Parameters:
x –
Intervalfor \(x\)y –
Intervalfor \(y\)rho –
Intervalfor \(\rho\)theta –
Intervalfor \(\theta\)
x,y,rho,theta = Interval(1.5,2.5),Interval(4,11),Interval(7,8),Interval(0.6,1.45)
c = CtcPolar()
x,y,rho,theta = c.contract(x,y,rho,theta)
# x = [1.5, 2.5] ; y = [6.53834, 7.85812] ; rho = [7, 8] ; theta = [1.20558, 1.38218]
Interval x(1.5,2.5), y(4,11), rho(7,8), theta(0.6,1.45);
CtcPolar c;
c.contract(x,y,rho,theta);
// x = [1.5, 2.5] ; y = [6.53834, 7.85812] ; rho = [7, 8] ; theta = [1.20558, 1.38218]
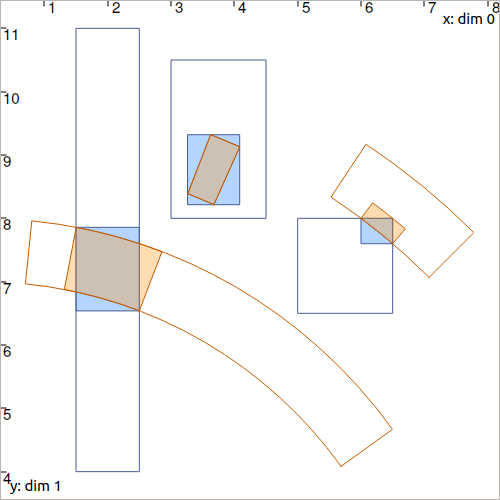
Illustration of several contracted boxes and pies with the CtcPolar contractor. The blue boxes \([x^i]\times[y^i]\) have been contracted as well as the pies \([\rho^i]\times[\theta^i]\). The above script examples are displayed in this figure.