Generic CtcFunction: \(\mathbf{f}(\mathbf{x})=\mathbf{0}\)

Lot of constraints can be expressed under the form \(\mathbf{f}(\mathbf{x})=\mathbf{0}\) with \(\mathbf{f}\) an analytic function possibly non-linear. The goal is to estimate the set of feasible vectors \(\mathbf{x}\) of a domain \([\mathbf{x}]\) that satisfy this constraint. A dedicated contractor can be built from \(\mathbf{f}\) in order to contract boxes.

Note that the other form \(\mathbf{f}(\mathbf{x})\in[\mathbf{y}]\) can also be treated by this contractor.

Contents

• Generic CtcFunction: \(\mathbf{f}(\mathbf{x})=\mathbf{0}\)

  • Definition

  • Example

  • Another example

  • Dealing with inequalities

  • Going further

Definition

Important

\[\mathbf{f}(\mathbf{x})=\mathbf{0} \longrightarrow \mathcal{C}_{\mathbf{f}}\big([\mathbf{x}]\big) \mathrm{~~~~or~~~~} \mathbf{f}(\mathbf{x})\in[\mathbf{y}] \longrightarrow \mathcal{C}_{\mathbf{f},[\mathbf{y}]}\big([\mathbf{x}]\big)\]

Python

C++

# For the constraint f(x)=0
ctc_f = CtcFunction(Function("<var1>", "<var2>", ..., "<expr>"))
ctc_f.contract(x)

# For the constraint f(x)ϵ[y]
y = Interval(...) # or IntervalVector if f is a vector function
ctc_f = CtcFunction(Function("<var1>", "<var2>", ..., "<expr>"), y)
ctc_f.contract(x)

// For the constraint f(x)=0
CtcFunction ctc_f(Function("<var1>", "<var2>", ..., "<expr>"));
ctc_f.contract(x);

// For the constraint f(x)ϵ[y]
Interval y(...); // or IntervalVector if f is a vector function
CtcFunction ctc_f(Function("<var1>", "<var2>", ..., "<expr>"), y);
ctc_f.contract(x);

Note

This contractor originates from the IBEX library. It is briefly presented here for the sake of consistency. For more information, please refer to the IBEX documentation for C++.

Optimality

This contractor is not necessarily optimal, depending on the expression of \(\mathbf{f}\).

Example

The constraint:

\[x_1+x_2=x_3\]

is equivalent to:

\[f(\mathbf{x})=0 \mathrm{~~~with~~~} f(\mathbf{x})=x_1+x_2-x_3\]

We can then build the contractor with:

Python

C++

ctc_f = CtcFunction(Function("x1", "x2", "x3", "x1+x2-x3"))

CtcFunction ctc_f(Function("x1", "x2", "x3", "x1+x2-x3"));

Another example

Let us consider the following non-linear function:

\[f(\mathbf{x}) = x_1\cos(x_1-x_2)\sin(x_1)+x_2\]

A contractor for the constraint \(f(\mathbf{x})=0\) can be built by:

Python

C++

ctc_f = CtcFunction(Function("x1", "x2", "x1*cos(x1-x2)*sin(x1)+x2"))

CtcFunction ctc_f(Function("x1", "x2", "x1*cos(x1-x2)*sin(x1)+x2"));

The first parameters are the variables names. The last one is the expression of \(f\).

Note that it is also possible to write vector variables:

Python

C++

ctc_f = CtcFunction(Function("x[2]", "x[0]*cos(x[0]-x[1])*sin(x[0])+x[1]"))

CtcFunction ctc_f(Function("x[2]", "x[0]*cos(x[0]-x[1])*sin(x[0])+x[1]"));

Then, a box \([\mathbf{x}]\) can be contracted by:

Python

C++

x = IntervalVector([[-2,-1],[1,2.5]])
ctc_f.contract(x)

IntervalVector x({{-2.,-1.},{1.,2.5}});
ctc_f.contract(x);

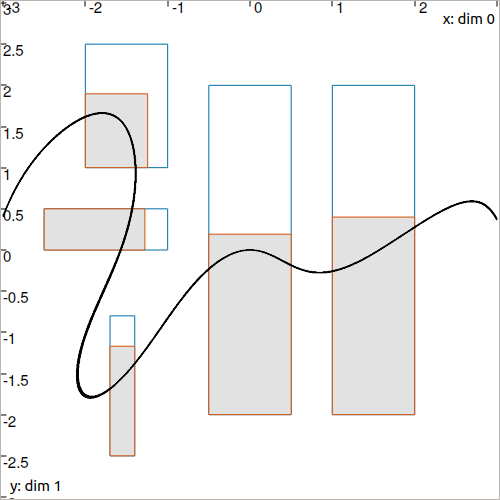
The boxes are contracted in order to remove some vectors that are not consistent with \(f(\mathbf{x})=0\). In the following figure, the exact solution for \(f(\mathbf{x})=0\) is black painted. The initial boxes are depicted in blue, their contraction is represented in red.

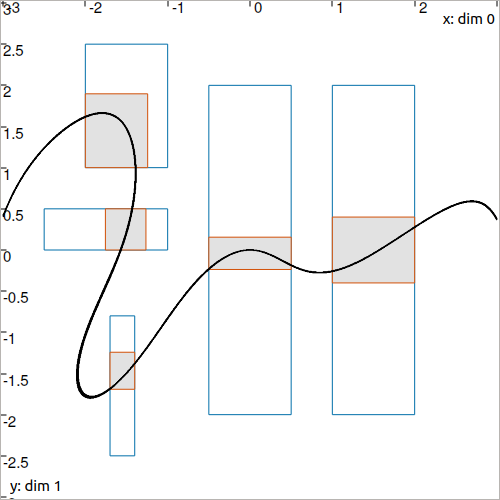
Fig. 15 Illustration of several contracted boxes with the above ctc_f contractor.

Dealing with inequalities

For constraints under the form \(\mathbf{f}(\mathbf{x})\in[\mathbf{y}]\) (instead of \(\mathbf{f}(\mathbf{x})=\mathbf{0}\) as in the previous section), one can specify \([\mathbf{y}]\) as last optional argument of CtcFunction.

A constraint \(\mathbf{f}(\mathbf{x})\leqslant 0\) is equivalent to \(\mathbf{f}(\mathbf{x})\in[-\infty,0]\) and so the related contractor becomes:

Python

C++

ctc_f = CtcFunction(Function("x[2]", "x[0]*cos(x[0]-x[1])*sin(x[0])+x[1]"), Interval(-oo,0))

CtcFunction ctc_f(Function("x[2]", "x[0]*cos(x[0]-x[1])*sin(x[0])+x[1]"), Interval(-oo,0));

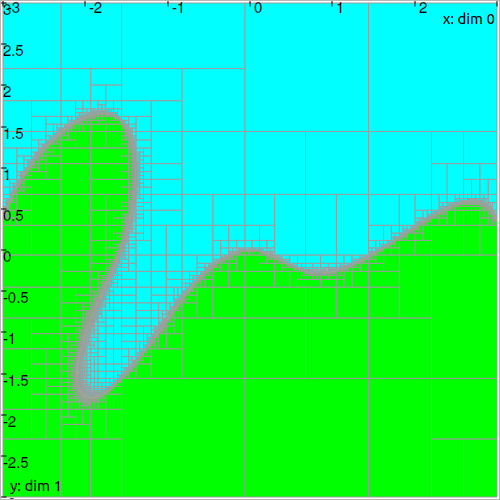
The above illustration reveals several contracted boxes with the new ctc_f contractor, in the case of inequalities. The actual solution set \(\mathbb{X}=\{\mathbf{x}\mid\mathbf{f}(\mathbf{x})\leqslant 0\}\) is green painted.

Going further

This CtcFunction class is a generic shortcut to deal with \(\mathbf{f}(\mathbf{x})=\mathbf{0}\) or \(\mathbf{f}(\mathbf{x})\in[\mathbf{y}]\). However, several algorithms exist to optimally deal with different classes of problems. A list of static contractors is provided in the IBEX library: see more. The user is invited to use an appropriate tool to deal with the constraint at stake.

The IBEX contractor behind CtcFunction is a CtcFwdBwd coupled with a Ctc3BCid.

Technical documentation

See the C++ API documentation of this class.