See also
This manual refers to Codac v1, but a new v2 implementation is currently in progress… an update of this manual will be available soon. See more.
CtcConstell: \(\mathbf{x}\in\mathbb{M}\)
The constellation contractor, denoted by \(\mathcal{C}_\textrm{constell}\), is used to solve the data association problem. Given a list of vectors \(\mathbf{m}_{1}\), \(\dots\), \(\mathbf{m}_{\ell}\) forming a constellation, the contractor reduces a box \([\mathbf{x}]\) to perfectly wrap the vectors previously enclosed inside of it.
Context
In robotics, when several landmarks \(\mathbf{m}_{1}\), \(\dots\), \(\mathbf{m}_{\ell}\) exist, the observation data may not be associated: we do not know to which landmark a given measurement \(\mathbf{y}\) refers. In other words it may be difficult, from the perception of a landmark, to find its identity only from the measurement data. However, data fusion can be done (for instance, by merging information coming from robot’s evolution). From fusion, we can obtain that the perceived landmark belongs to a reduced set of landmarks \([\mathbf{x}]\). The contractor presented here simply aims at reducing optimally this prior set \([\mathbf{x}]\) to finally perfectly wrap the vectors inside of it, thus allowing further contractions.
Definition
Let us consider a constellation of \(\ell\) points \(\mathbb{M}=\{[\mathbf{m}_{1}],\dots,[\mathbf{m}_{\ell}]\}\) of \(\mathbb{IR}^{d}\) and a box \(\left[\mathbf{x}\right]\in\mathbb{IR}^d\). We want to compute the smallest box \(\mathcal{C}_\textrm{constell}\left(\left[\mathbf{x}\right]\right)\) containing \(\mathbb{M}\cap\left[\mathbf{x}\right]\), or equivalently:
where \(\bigsqcup\), called squared union, returns the smallest box enclosing the union of its arguments.
Important
ctc_constell = CtcConstell(v_b) # with v_b, the vector defining
# the constellation of points
#include <codac-rob.h>
CtcConstell ctc_constell(v_b); // with v_b, the vector<IntervalVector> defining
// the constellation of points
Example
Let us consider the following constellation:
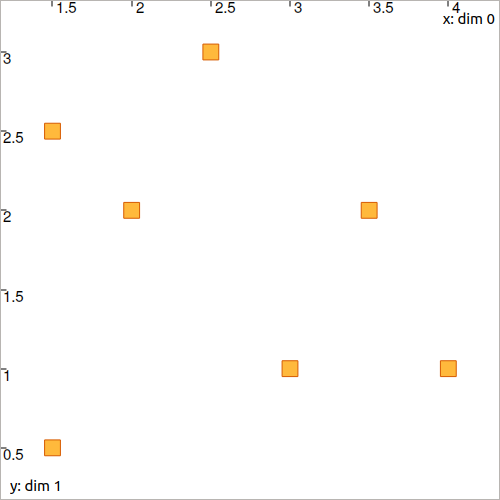
Fig. 18 A given constellation of points \(\big\{[\mathbf{m}_1],\dots,[\mathbf{m}_\ell]\big\}\).
The \(\mathcal{C}_\textrm{constell}\) can be instantiated with
v_b = [... // vector defining the constellation of points
ctc_constell = CtcConstell(v_b)
#include <codac-rob.h>
// ...
vector<IntervalVector> v_b; // vector defining the constellation of points
v_b.push_back( // ...
CtcConstell ctc_constell(v_b);
Now, if we define three boxes:
v_x = [IntervalVector([[1.25,3],[1.6,2.75]]), \
IntervalVector([[2.,3.5],[0.6,1.2]]), \
IntervalVector([[1.1,3.25],[0.2,1.4]])]
vector<IntervalVector> v_x;
v_x.push_back({{1.25,3},{1.6,2.75}});
v_x.push_back({{2.,3.5},{0.6,1.2}});
v_x.push_back({{1.1,3.25},{0.2,1.4}});
we can use the \(\mathcal{C}_\textrm{constell}\) to contract them according to the constellation.
for x in v_x:
ctc_constell.contract(x)
for(auto& x : v_x)
ctc_constell.contract(x);
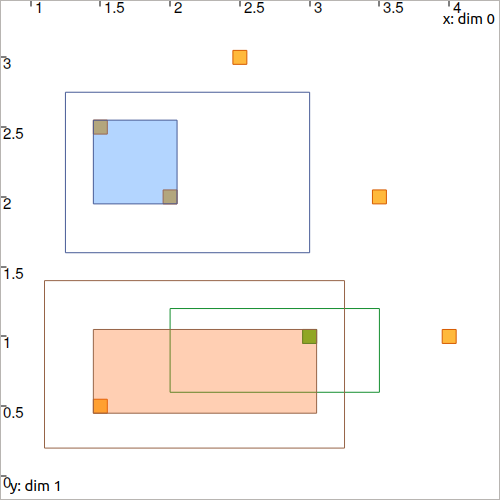
Fig. 19 Filled boxes are the \([\mathbf{x}]\) after contraction.