See also

This manual refers to Codac v1, but a new v2 implementation is currently in progress… an update of this manual will be available soon. See more.

Set-inversion and separators

A separator \(\mathcal{S}\) is an operator that performs two complementary contractions. Associated with a set \(\mathbb{S}\) and given a box \([\mathbf{x}]\), the separator produces two sub-boxes \([\mathbf{x}_ {in}]\) and \([\mathbf{x}_{out}]\) that verify:

\[\begin{split}([\mathbf{x}] \cap [\mathbf{x}_{in}]) \subset \mathbb{S} \\ ([\mathbf{x}] \cap [\mathbf{x}_{out}]) \cap \mathbb{S} = \varnothing\end{split}\]

A separator can also be viewed as a pair of contractors. For efficiency reasons, the .separate(…) method takes only two input-output arguments, \([\mathbf{x}_{in}]\) and \([\mathbf{x}_{out}]\), each containing initially a copy of the box \([\mathbf{x}]\).

Separators can be combined and involved in an algorithm for set-inversion such as SIVIA. An example of set-inversion of a non-linear function using separators is provided below:

PythonC++

from codac import *
from vibes import vibes

# Define some non-linear function
f = Function('x', 'y', 'x*cos(x-y)+y')

# Build the separator associated to the constraint f(x,y) < 0
sep = SepFunction(f, [-oo,0])

# Graphics
vibes.beginDrawing()
vibes.newFigure("Set inversion")
vibes.setFigureProperties({"x":100, "y":100, "width":500, "height":500})
SIVIA([[-10, 10],[-10, 10]], sep, 0.21, fig_name="Set inversion")
vibes.endDrawing()

The set-inversion leads to the following paving:

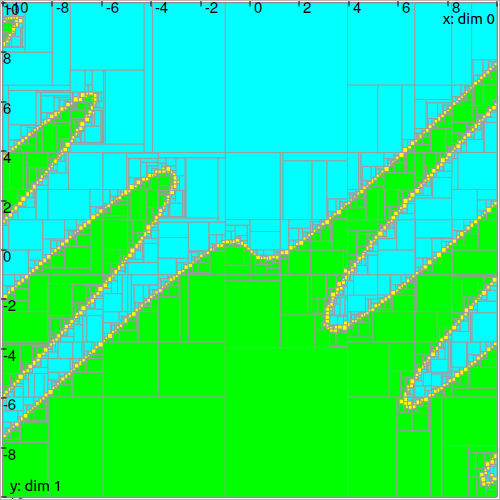
Fig. 49 Set-inversion of the function \(f(x,y)=x\cdot\cos(x-y)+y\), considering the constraint \(f(x,y)\leqslant 0\) (which can be formalized as \(f(x,y)\in[-\infty,0]\)).

Green boxes only enclose vectors that are solutions of the inequality, blue ones do not contain solutions, and the yellow fronteer contains the boundary of the solution set.

The SIVIA(..) function allows several parameters for specifying result outputs (returned values, displayed colors). For instance:

PythonC++

SIVIA(box,              # initial domain to be bisected
  sep,                  # related separator (or contractor if provided)
  0.21,                 # precision parameter (stopping condition)
  regular_paving=False, # keep a regular paving (bisection rule)
  display_result=True,  # displaying boxes in a VIBes figure
  fig_name="SIVIA",     # name of the VIBes figure in case of display
  return_result=True,   # returning a map of lists of boxes
  # The following color map allows to define custom colors for subpavings:
  color_map={SetValue.IN:"k[r]", SetValue.OUT:"k[b]", SetValue.UNKNOWN:"k[y]"})

Separators

The following separators apply on intervals and boxes:

• SepBox: \(\mathcal{S}_{box}\)
  • Definition
  • Example

See also: codac-unsupported.