codac2_Interval_operations.h File Reference

#include "codac2_Interval.h"
#include "codac2_Interval_operations_impl.h"

Include dependency graph for codac2_Interval_operations.h:

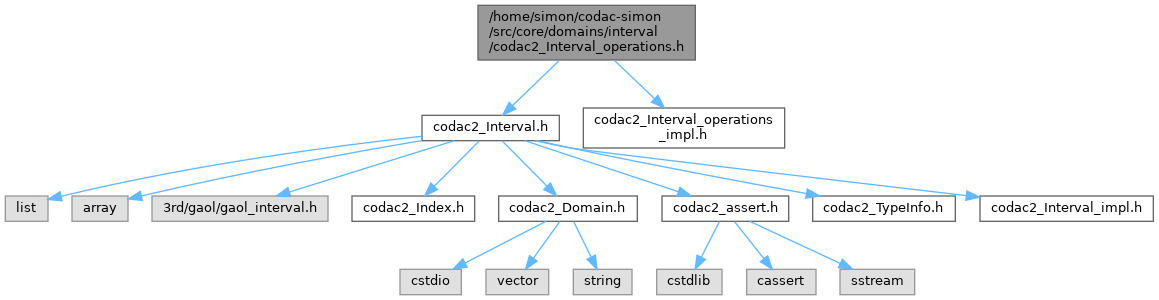
This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Namespaces
namespace	codac2

Functions
Interval	codac2::sqr (const Interval &x)
	Returns \([x]^2\).
Interval	codac2::sqrt (const Interval &x)
	Returns \(\sqrt{[x]}\).
Interval	codac2::pow (const Interval &x, int n)
	Returns \([x]^n\), \(n\in\mathbb{Z}\).
Interval	codac2::pow (const Interval &x, double p)
	Returns \([x]^p\), \(p\in\mathbb{R}\).
Interval	codac2::pow (const Interval &x, const Interval &p)
	Returns \([x]^{[p]}\), \(p\in\mathbb{IR}\).
Interval	codac2::root (const Interval &x, int p)
	Returns the p-th root: \(\sqrt[p]{[x]}\).
Interval	codac2::exp (const Interval &x)
	Returns \(\exp([x])\).
Interval	codac2::log (const Interval &x)
	Returns \(\log([x])\).
Interval	codac2::cos (const Interval &x)
	Returns \(\cos([x])\).
Interval	codac2::sin (const Interval &x)
	Returns \(\sin([x])\).
Interval	codac2::tan (const Interval &x)
	Returns \(\tan([x])\).
Interval	codac2::acos (const Interval &x)
	Returns \(\acos([x])\).
Interval	codac2::asin (const Interval &x)
	Returns \(\asin([x])\).
Interval	codac2::atan (const Interval &x)
	Returns \(\atan([x])\).
Interval	codac2::atan2 (const Interval &y, const Interval &x)
	Returns \(\mathrm{arctan2}([y],[x])\).
Interval	codac2::cosh (const Interval &x)
	Returns \(\cosh([x])\).
Interval	codac2::sinh (const Interval &x)
	Returns \(\sinh([x])\).
Interval	codac2::tanh (const Interval &x)
	Returns \(\tanh([x])\).
Interval	codac2::acosh (const Interval &x)
	Returns \(\acosh([x])\).
Interval	codac2::asinh (const Interval &x)
	Returns \(\asinh([x])\).
Interval	codac2::atanh (const Interval &x)
	Returns \(\atanh([x])\).
Interval	codac2::abs (const Interval &x)
	Returns \(\mid[x]\mid = \left\{\mid x \mid, x\in[x]\right\}\).
Interval	codac2::min (const Interval &x, const Interval &y)
	Returns \(\min([x],[y])=\left\{\min(x,y), x\in[x], y\in[y]\right\}\).
Interval	codac2::max (const Interval &x, const Interval &y)
	Returns \(\max([x],[y])=\left\{\max(x,y), x\in[x], y\in[y]\right\}\).
Interval	codac2::sign (const Interval &x)
	Returns \(\sign([x])=\left[\left\{\sign(x), x\in[x]\right\}\right]\).
Interval	codac2::integer (const Interval &x)
	Returns the largest integer interval included in \([x]\).
Interval	codac2::floor (const Interval &x)
	Returns floor of \([x]\).
Interval	codac2::ceil (const Interval &x)
	Returns ceil of \([x]\).
Interval	codac2::chi (const Interval &x, const Interval &y, const Interval &z)
	Return \([y]\) if \(x^+ <= 0\), \([z]\) if \(x^- > 0\), \([y]\sqcup[z]\) else.

Detailed Description

This class reuses several functions developed for ibex::Interval. See ibex::Interval (IBEX lib, main author: Gilles Chabert) https://ibex-lib.readthedocs.io

---

Date

2024

Author

Gilles Chabert, Simon Rohou

Copyright

Copyright 2024 Codac Team

License: GNU Lesser General Public License (LGPL)