codac2_inversion.h File Reference
Include dependency graph for codac2_inversion.h:
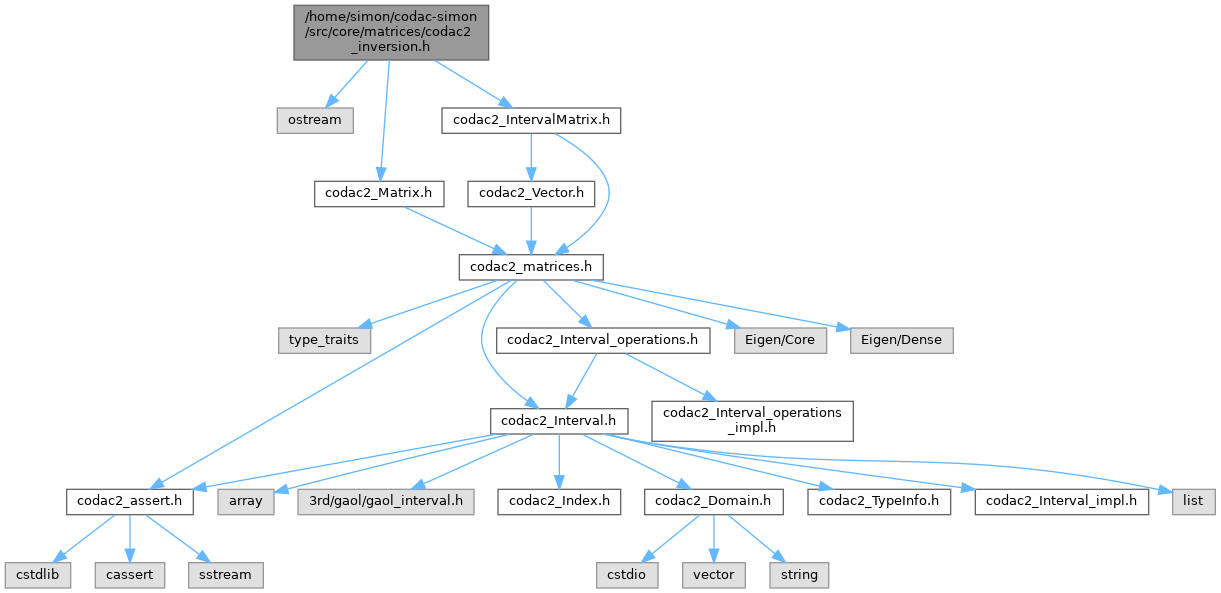
Go to the source code of this file.
Namespaces | |
| namespace | codac2 |
Functions | |
| template<LeftOrRightInv O = LEFT_INV, typename OtherDerived, typename OtherDerived_> | |
| IntervalMatrix | codac2::inverse_correction (const Eigen::MatrixBase< OtherDerived > &A, const Eigen::MatrixBase< OtherDerived_ > &B) |
| Correct the approximation of the inverse \(\mathbf{B}\approx\mathbf{A}^{-1}\) of a square matrix \(\mathbf{A}\) by providing a reliable enclosure \([\mathbf{A}^{-1}]\). | |
| template<typename OtherDerived> | |
| IntervalMatrix | codac2::inverse_enclosure (const Eigen::MatrixBase< OtherDerived > &A) |
| Enclosure of the inverse of a (non-singular) matrix expression, possibly an interval matrix. | |
| IntervalMatrix | codac2::infinite_sum_enclosure (const IntervalMatrix &A, double &mrad) |
| Compute an upper bound of \(\left([\mathbf{A}]+[\mathbf{A}]^2+[\mathbf{A}]^3+\dots\right)\), with \([\mathbf{A}]\) a matrix of intervals as an "error term" (uses only bounds on coefficients). | |
Detailed Description
- Date
- 2024
- Copyright
- Copyright 2024 Codac Team
- License: GNU Lesser General Public License (LGPL)
Generated by